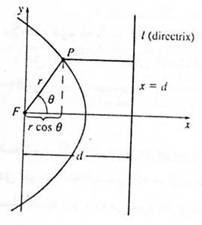
حال می خواهیم معادله ی بیضی را در دستگاه مختصات قطبی پیدا کنیم .

 اینگونه است .e را برون مرکزی بیضی می نامند و با رابطه ی بالا می شناسند . در مختصات قطبی e

=e

در جریان محاسبه می بینیم که این رابطه درست است . پس داریم .

 و می دانیم که

2 طرف را مربع می کنیم عبارات بالا را جایگزین می کنیم .

 فاکتور   را به سمت چپ می بریم و از  و   را در پرانتز اثر می دهیم و عبارات

می گیریم .

 را اضافه می کنیم . این عمل را تقسیم می کنیم . به 2 طرف عبارت 2 طرف را بر عبارت

انجام دادیم تا عبارت زیر بدست آید .

اگر عبارات زیر را داشته باشیم :

 ,  ,

عبارت به صورت زیر در می آید :

 را می نویسیمe درست است eکه معادله ی یک بیضی است حال برای آنکه بدانیم تعریف ما از

همان چیزی که انتظار آن را داشتیم پس معادله ی بیضی در دستگاه مختصات قطبی چنین است :

اثبات قوانین کپلر :

قانون اول :

همانطور که قبلا نیز گفته شد قانون اول بیان می کند که هر جسمی که تحت تاثیر نیروی گرانش جسم دیگری باشد در مداری بیضوی دور آن می چرخد .

2 اثبات برای این قانون اینجا ذکر می کنیم .

اثبات 1 :

برای اثبات این که سیاره بیضوی می چرخد ابتدا باید ثابت کنیم که در یک صفحه می چرخد لذا داریم

 قانون دوم نیوتن :

 قانون گرانش نیوتن :

ابتدا باید عرض کنم حروفی که کج نوشته شده اند نشاندهنده ی اندازه اند و حروفی که به صورت معمولی نوشته شده اند نشاندهنده ی بردار اند .

 جرم سیارات به ترتیب جرم دور زننده و جرم ثابت می باشندM و m  نیروی گرانشی روی سیاره ، F

 می باشد .r بردار یکه در سوی  و  ثابت گرانش ، G

 های 2 قانون را برابر با هم قرار می دهیم .F

 ها از طرفین ساده می شوند .m

 است پس موازیند و داریم .r ضریبی از بردار aو بنابراین می فهمیم که بردار

 بردار سرعت است بنابر این داریم :v

 بر 2 بردارh نتیجه می شود که بردار ثابت  یک بردار ثابت است و حال اگر فرض کنیم که hکه در آن

 هر دو در یک صفحه اند .v و بردار r عمود است پس بردار v و r

می دانیم که بردار سرعت همواره بر مسیر حرکت مماس می باشد پس مدار بر یک صفحه قرار دارد .

 شروع می کنیم به اثبات قانون اول کپلر داریم :hاز بردار ثابت

پس بنابر این داریم :

قضیه ای است در مورد ضرب خارجی که بیان می کند که :

جای اثبات این قضیه نیست آن را می پذیریم و ادامه می دهیم .

داشته باشد آنگاه بردار مکان بر بردار مماس آن عمود است پس در در اینجا

با انتگرال گیری از 2 طرف داریم :

 یک بردار ثابت است .cکه در آن

 باشد مناسب h در سوی بردار Kدر اینجا انتخاب محور های مختصات به طوری که بردار پایه استاندارد

 عمودند برابری بالا h بر u و  حرکت می کند . چون هر دوی xyاست . در این صورت سیاره در صفحه

 را طوری انتخاب کنیم که y و محور x قرار دارد یعنی می توانیم محور xy در صفحه cنشان می دهد که

 قرار گیرد .c در سوی iهمان طور که در شکل نشان داده شده است بردار